The Expert Guide to ISEE Quantitative Reasoning: Strategies, Tips, and Examples
/ISEE QR SAMPLE QUESTION
The Independent School Entrance Exam (ISEE) has two sections that test mathematical ability. The first of the two is ISEE Quantitative Reasoning, designed to measure a student’s ability to reason and think logically about mathematics.
Very little to no calculation is required on ISEE Quantitative Reasoning, and a calculator is not permitted.
Questions may assess the ability to estimate values, compare and contrast quantities, analyze and interpret data, summarize graphs, determine probability, understand concepts and applications of measurement, and answer questions relating to geometry.
In this article, we’ll take a closer look at ISEE Quantitative Reasoning question types and how to prepare for this section of the assessment.
How Many Questions Does the Quantitative Reasoning Section Ask?
The number of Quantitative Reasoning questions you’ll need to answer differs very slightly by grade level. There are three main levels of the ISEE:
35 minutes are allotted for the Quantitative Reasoning section at all three levels. However, Lower Level students answer 38 questions, while Upper and Middle Level test-takers are given 37 questions.
What Type of Questions Does ISEE Quantitative Reasoning Ask?
The Quantitative Reasoning section of the ISEE is mostly comprised of word problems. Upper and Middle Level students must also answer 17 Quantitative Comparison questions (a little less than half of questions in the section).
Quantitative Comparison questions all have the same four answer choices:
Both ISEE math sections are linked to the standards of the National Council of Teachers of Mathematics (NCTM). The test uses six NCTM “strands” as a basis for its math questions. These strands are:
Let’s take a closer look at the six strands, including examples of each.
Numbers and Operations
To adequately answer these questions, Lower Level students must be able to accurately add, subtract, multiply, and divide. They must also understand numbers and various ways to represent numbers.
Middle Level students must be able to “analyze, perform operations on, and compare integers, fractions, decimals, and percentages.”
For Upper Level students, these questions require an understanding of numbers, relationships among numbers, meanings of operations, and relationships among operations.
The following is an example of a Middle Level “Numbers and Operations” question developed by the Educational Records Bureau (ERB), who also designs the ISEE.
This question can be solved by setting up a proportion. Otherwise, you can recognize that if 40% of the apples are red, 60% must be green. The six red apples comprise 40% of the basket, meaning we can determine that every 3 apples is equal to 20% of the total apples in the basket. Since 60% of the apples are green, there must be 9 green apples, meaning the answer is C.
From this example, you can see that these questions are more about mathematical logic rather than mathematical calculation.
Algebraic Concepts
Lower Level students simply need the ability to find and extend rules for patterns and relationships.
Middle Level students must interpret and evaluate patterns, functions, and relationships, as well as creating representations of these mathematical situations.
At the Upper Level, students are asked to represent and analyze algebraic, graphical, and other mathematical situations involving patterns, functions, and relationships.
A Lower Level “Algebraic Concepts” question might look something like this:
The correct answer is C. First, we must multiply 2 and 6 to represent that Jim bought two boxes of nails for $6. That narrows it down to C and D, but Jim only bought one hammer, so we add “h” instead of “2h,” making C the answer.
To give you an idea of what Middle and Upper Level Quantitative Comparison questions look like, here’s an Upper Level Quantitative Comparison question focusing on Algebraic Concepts.
A great strategy to use when solving Quantitative Comparison questions is to plug in a few different values for x, including both positive and negative numbers.
In this case, the greater quantity varies according to what value is used to represent x. Therefore, the correct answer is D. We don’t know enough information to determine which quantity is greater.
Geometry
For Geometry questions, Lower Level test-takers are required to identify and describe geometric objects and their characteristics. For example, students may need to know about symmetry or the number of sides and vertices in various shapes.
Middle Level students should be able to understand and describe geometric shapes and figures, as well as their characteristics and properties.
To answer Upper Level Geometry questions, students must analyze the characteristics of geometric figures and visualize and describe the spatial relationships of geometric objects. Consider the example below.
In order to answer this question correctly, an Upper Level student should know that the interior angle of a regular quadrilateral is 90 degrees, while the interior angle of a regular hexagon measures 120 degrees.
Alternatively, a student could know enough about geometry to reason that the addition of two sides would result in wider angles.
Either way, the correct answer is B: the quantity in Colum B is greater.
Measurement
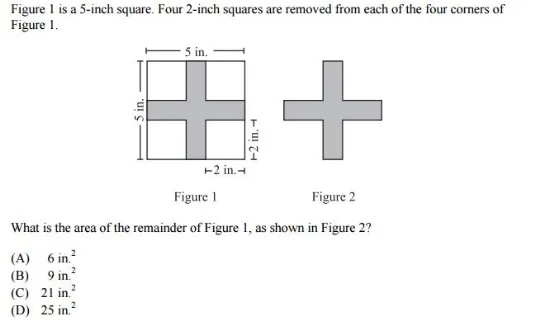
Lower Level students should be able to understand and determine measurable characteristics of objects, as in the example below:
This problem seems complex, but only logic and simple mathematics are required to solve it. First, you must recognize that the question is asking you to calculate the area of 5x5 inch square after four corners are removed.
First, find the total area of the square by multiplying 5(5), which equals 25 square inches.
Next, you can calculate that the area of one 2x2 corner is 4 inches squared. This means that the area of all four corners must be 16 square inches.
To determine the area of the remainder of the figure once the four corners have been removed, you would simply subtract 16 (the total area of the four corners) from 25 (the total area of the square itself). The answer is therefore B: 9 inches squared.
Middle Level students need to understand and use formulas for the measurable attributes of objects. For example, a Middle Level test-taker may be asked to compare the areas of two triangles with differing scale factors.
At the Upper Level, students are expected to develop, analyze, and use their own formulas for the measurable attributes of objects.
The skills required at each level naturally build on one another, just like the standards of the National Council of Teachers of Mathematics.
Data Analysis and Probability
Both Lower Level and Middle Level students should be able to collect, display, interpret, and make predictions about a set of data. However, while Lower Level students must find the probability of a simple event, Middle Level test-takers are required to apply the basic concepts of probability.
Upper Level students are asked to analyze, interpret, and make inferences about a set of data, in addition to applying more complex concepts of probability.
The following example is a Middle Level Probability question.
The correct answer in this case is C. You must first understand that there are 12 possible sums.
Since the sum of 3 appears twice, the probability that the sum will be 3 is 2/12, or 1/6.
The sum of 6 also appears twice, so the probability is again 2/12, or 1/6.
This means that the two values are equal.
Problem Solving
There are no particular questions or skills required for Problem Solving, as this skill is measured by all ISEE Quantitative Reasoning questions.
Students must have an understanding of grade-level appropriate mathematical concepts and the ability to logically reason in order to solve the problems presented on this section of the assessment.
Although solving these problems is considered challenging, there are strategies you can use to increase your chances of success.
What Strategies Can I Use to Score High on ISEE Quantitative Reasoning?
There are several basic test-taking strategies—some that specifically apply to mathematics questions—that you can use to master ISEE Quantitative Reasoning.
Write in the test book.
This strategy is especially effective for math questions. If you’re taking the test on paper, feel free to write all over the test book. If you’re taking the exam on the computer, the same is true for the scratch paper you’ll be given.
Underline and circle key words, write out the problems, draw pictures, and do anything else that may help you solve each problem.
Writing out your work can help you visualize your thought process and arrive at a faster, more accurate answer to the question. Nothing in your test book or scratch paper will be scored, so work out the problems using whatever method works best for you.
Plug and chug.
When possible, plug the answer choices into the question to see which choice actually makes sense or answers the question logically.
For Quantitative Comparison questions involving variables, plug in a variety of numbers, both positive and negative, for x to determine whether the value in Column A or the value in Column B is greater.
This strategy is a shortcut that can help you get to the correct answer as quickly as possible. This is a major advantage, since you’ll have a minute or less per question.
Use process of elimination.
Sometimes, an answer choice is clearly much too big, much too small, or simply illogical for the question being asked.
In that case, use process of elimination by crossing out obviously wrong answers. This narrows down your answer choices, meaning that if you end up having to guess, at least you’ll be able to make an educated guess.
Since we’re talking math, any answer choice you eliminate increases your chances of answering the question correctly by 25%.
Skip difficult questions and return to them later.
Since you have a minute or less for each question on ISEE Quantitative Reasoning, timing is crucial. If you find yourself stuck on a question, skip it and come back to it after answering easier questions.
There is no reason to waste excessive amounts of time on a challenging question that you may not answer correctly. Just be sure to mark the question with an asterisk or circle so you remember to come back to it, and leave a space on your answer sheet.
If you have to skip a question, don’t panic. The ISEE is notoriously difficult, and no one is expected to answer every single question correctly. Mentally remind yourself that you’re capable and prepared, and continue working with a positive attitude.
Answer every question.
There is no penalty for guessing incorrectly on the ISEE, so you should answer every single question on the test.
Even if time is running out and you have ten unanswered questions, quickly go through and bubble something for every blank question.
You’re not going to get all of them right, but you’ll probably pick up a couple of extra points, and a couple of extra points can make a big difference.
What Long-Term Strategies Can I Use to Be Successful on ISEE Quantitative Reasoning?
In addition to the test-taking strategies we’ve just mentioned, there are also a couple of long-term strategies you can use to turn in a successful performance on ISEE Quantitative Reasoning.
Work hard in your math class.
Although this section of the test focuses on mathematical reasoning abilities rather than calculation, you will still need solid knowledge of grade-level appropriate mathematical concepts.This includes vocabulary and processes that students in your grade level should understand.
For that reason, it’s important that you pay attention in math class throughout the year. Take notes, complete your classwork and homework, and consistently study the material.
If you find yourself struggling, ask your teacher for extra help or get a math tutor. Working hard and understanding grade-level math throughout the year will make ISEE Quantitative Reasoning much easier for you.
Complete practice questions.
The easiest way to build confidence and familiarity with the ISEE is by completing practice questions or full-length practice tests.
You can download free ISEE practice tests below. These tests are made by the the Educational Records Bureau, or the ERB, and are the gold standard for ISEE practice tests.
Just click one of the buttons below to get access to the tests, plus you will also receive our 5 proven test prep strategies for using official ISEE practice tests to effectively prepare.
Get Upper Level ISEE Practice Test
Get Middle Level ISEE Practice Test
Get Lower Level ISEE Practice Test
When you first start working with practice questions, don’t time yourself. Simply start figuring out what strategies work for you and how you plan to approach different question types.
As you start feeling more comfortable, try timing yourself to get a sense of how you will need to pace yourself on the test. If you’re going too slowly, work on figuring out shortcuts to answer questions more efficiently.
When you miss questions, make sure you take the time to understand why your answer was incorrect and the right answer is correct. Think about how you will approach these questions differently in the future.
Work hard in math class, answer practice questions, and use smart test-taking strategies, and you should be well on your way to conquering ISEE Quantitative Reasoning.